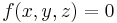Quartic surface

In mathematics, especially in algebraic geometry, a quartic surface is a surface defined by an equation of degree 4.

More specifically there are two closely related types of quartic surface: affine and projective. An affine quartic surface is the solution set of an equation of the form

where f is a polynomial of degree 4, such as f(x,y,z) = x⁴ + y⁴ + xyz + z² − 1. This is a surface in affine space.

On the other hand, a projective quartic surface is a surface in projective space P³ of the same form, but now f is a homogeneous polynomial of 4 variables of degree 4, so for example f(x,y,z,w) = x⁴ + y⁴ + xyzw + z²w² − w⁴.

If the base field in R or C the surface is said to be real or complex. If on the other hand the base field is finite, then it is said to be an arithmetic quartic surface.

Special quartic surfaces

• Dupin cyclides
• The Fermat quartic, given by x⁴ + y⁴ + z⁴ + w⁴ =0 (an example of a K3 surface) – and tiled by 12 octagons, in the Dyck tiling (named after Walther von Dyck).
• K3 surfaces
• Klein quartic
• Kummer surface
• Plücker surface
• Weddle surface

See also

• Quadric surface (The union of two quadric surfaces is a special case of a quartic surface)
• Cubic surface (The union of a cubic surface and a plane is another particular type of quartic surface)

References

• Hudson, R. W. H. T. (1990), Kummer's quartic surface, Cambridge Mathematical Library, Cambridge University Press, ISBN 978-0-521-39790-2, MR1097176, http://www.archive.org/details/184605691 
• Jessop, C. M. (1916), Quartic surfaces with singular points, Cornell University Library, ISBN 978-1-4297-0393-2, http://digital.library.cornell.edu/cgi/t/text/text-idx?c=math;idno=04290002